User:Jorend/Deterministic hash tables
Contents
Abstract
A deterministic hash table proposed by Tyler Close was implemented in C++ and its performance was compared to two hash table implementations using open addressing. Speed and memory usage were measured.
Speed. The Close table implementation was very fast, faster than the open addressing implementations. (It is unclear why; theory suggests it "should" be slower, and measurement confirms that the Close table is doing more memory accesses and more branches. More investigation is needed!)
Memory. The Close table implementation always allocates more memory than the leanest open addressing implementation. See the Results section for details.
Background
Most hash table APIs (including C++'s unordered_map, Java's java.util.HashMap, Python's dict, Ruby's Hash, and many others) allow users to iterate over all the entries in the hash table in an arbitrary order. This exposes the user to an aspect of the library's behavior (the iteration order) that is unspecified and indeed intentionally arbitrary.
Map and Set data structures are proposed for a future version of the ECMAScript programming language. The standard committee would like to specify deterministic behavior if possible. There are several reasons for this:
- There is evidence that some programmers find arbitrary iteration order surprising or confusing at first. [1][2][3][4][5][6]
- Property enumeration order is unspecified in ECMAScript, yet all the major implementations have been forced to converge on insertion order, for compatibility with the Web as it is. There is, therefore, some concern that if TC39 does not specify a deterministic iteration order, “the web will just go and specify it for us”.[7]
- Hash table iteration order can expose some bits of object hash codes. This imposes some astonishing security concerns on the hashing function implementer. For example, an object's address must not be recoverable from the exposed bits of its hash code. (Revealing object addresses to untrusted ECMAScript code, while not exploitable by itself, would be a bad security bug on the Web.)
Can a data structure retain the performance of traditional, arbitrary-order hash tables while also storing the order in which entries were added, so that iteration order is deterministic?
Tyler Close has developed a deterministic hash table that is structured like this (pseudocode):
struct Entry {
Key key;
Value value;
Entry *chain;
}
class CloseTable {
Entry*[] hashTable; // array of pointers into the data table
Entry[] dataTable;
}
Lookups and inserts proceed much like a bucket-and-chain hash table, but instead of each entry being allocated separately from the heap, they are stored in the dataTable in insertion order.
Removing an entry simply replaces its key with some sentinel while leaving the chain intact.
Theory
Memory. Every map data structure must store the keys and values. A map with N entries must use at least NE memory, where E is the size of a key-value pair (we assume the data can’t be compressed).
In the following discussion we neglect the effect of deletions, which can cause both kinds of table to have extra memory that isn't in use at a given moment.
An open addressing hash table has additional overhead depending on the fill factor. OpenTable in particular has a maximum fill factor F=3/4. When it becomes more than 3/4 full, it doubles in size, becoming just over 3/8 full. The amount of overhead in an OpenTable is (1/f)NE, where f is the actual current fill ratio of the table and F/2 < f ≤ F.
A Close table has three sources of overhead: the entire hashTable, the chain pointers in the dataTable, and the unused portion of the dataTable. In CloseTable, the chain pointer causes each entry to require (3/2)E memory rather than E. The dataTable doubles in size when it becomes completely full, so its size is (3/2)(1/u)NE where u is the proportion of the dataTable that is in use and 1/2 < u ≤ 1. The hashTable is always 1/16 the size of the dataTable (1/8 on 64-bit platforms), so the total size of both tables is (1+1/16)(3/2)(1/u)NE (substitute 1/8 on 64-bit platforms).
For back-of-envelope purposes, then, f may be expected to be about 3F/4 (halfway between F/2 and F) and u about 3/4 on average; plugging these numbers in, we expect an OpenTable to use about (1/(3F/4)) = 1.78×NE, and a CloseTable about 2.13×NE (2.25×NE on 64-bit), on average. This would mean that the CloseTable would be 20% larger on average (27% larger on 64-bit). However, see the Results section for a picture of how the two implementations compare in practice.
Lookup speed. The get, has, set, and delete operations all start with a lookup. We will quantify lookup speed in terms of how many memory locations must be accessed. To simulate locality effects, we treat multiple reads from a single entry, or from the table object, as a single read.
In an open addressing hash table with fill factor f, an unsuccessful lookup performs about 1/(1-f) probes.[8] In an OpenTable, at worst f=F=3/4 and so an unsuccessful lookup performs 4 probes on average. In the usual case, f=3F/4=9/16, so about 2.3 probes on average. A successful lookup performs half as many probes on average. Before probing the table, the lookup must access the OpenTable struct itself, so the final numbers are as shown in the table: 5 reads, 3.3 reads, etc.
A Close table uses direct chaining. Each lookup must read first the CloseTable object itself, and next the hashTable. Then, for an unsuccessful lookup, the whole chain is walked; the expected length of the chain is simply the number of keys in the table divided by the number of hash buckets. For a CloseTable, this quotient is at most 8/3 and typically 2. A successful lookup would perform about half as many probes, if keys were distributed evenly, but instead they are distributed randomly, making successful lookups slower; by simulation, I found the expected number of probes is 2.3 under full load and 2 under typical load.
| Expected cost of unsuccessful lookup (miss) | Expected cost of successful lookup (hit) | |||
|---|---|---|---|---|
| Data structure | Maximum load | Typical load | Maximum load | Typical load |
OpenTable
| 5 | 3.3 | 3 | 2.2 |
CloseTable
| 4.7 | 4 | 4.3 | 4 |
Note: This analysis does not explain the lookup speed observed in practice. See the Results section.
Method
The code I used to make these pictures is available at: https://github.com/jorendorff/dht
The graphs below show data collected on a MacBook Pro, using g++-apple-4.2 and a 64-bit build. The results from running the test on a 32-bit Windows build were basically qualitatively the same. CloseTable performance was even better on Windows, for most tests; however, on LookupHitTest, OpenTable achieved almost equal speed.
The project contains two complete hash map implementations: OpenTable and CloseTable. A third implementation, DenseTable, is a thin wrapper around the dense_hash_map type from Sparsehash. The three classes have the same API and were all benchmarked using the same templates (in hashbench.cpp).
Hash table implementation design notes:
- The API was designed to match the proposal for ECMAScript Map objects as of February 2012.
- The Key and Value types are
uint64_tbecause ECMAScript values are 64 bits in the implementation I'm most familiar with.
- OpenTable and CloseTable are meant to be as fast and as memory-efficient as possible. Pretty much everything that can be omitted was omitted. For example, the hashing function is trivial: hash(key) = key, and neither OpenTable nor CloseTable further munges the hashcode before using it as a table index. Rationale: Making each implementation as fast as possible should highlight any performance difference between OpenTable and CloseTable, which is the purpose of the exercise. Using a more sophisticated hashing function would slow down both implementations, reducing the observed difference between the two techniques.
- DenseTable is provided as a baseline. (It's nice to have some realistic numbers in the graphs too.)
- dense_hash_map and OpenTable both implement straightforward hash tables with open addressing. The main difference between the two is one of tuning. dense_hash_map has a maximum load factor of 0.5. OpenTable has a maximum load factor of 0.75, which causes it to use about half as much memory most of the time.
- The purpose of the typedefs KeyArg and ValueArg is to make it possible to switch the API from pass-by-value to pass-by-reference by editing just a couple of lines of code. (I tried this. Pass-by-reference is no faster on 64-bit machines.)
- CloseTable attempts to allocate chunks of memory with sizes that are near powers of 2. This is to avoid wasting space when used with size-class-based malloc implementations.
- A Close table can trade some speed for compactness, but it seems to be a bad bargain:
- The load factor is adjustable. (The hash table size must remain at a power of two, but the data vector can have non-power-of-2 sizes.) However, increasing the load factor directly affects LookupMiss speed.
- An implementation could grow the data array by less than doubling it each time. I tried this. Insert speed suffered; lookup speed was unaffected; but the modified CloseTable still used more memory than OpenTable.
-
dense_hash_mapnever shrinks the table unless you explicitly ask it to.DenseTable::remove()periodically shrinks, because otherwise, the performance on LookupAfterDeleteTest is pathologically bad.
Benchmark design notes:
- The benchmark is pure C++, rather than a Map/Set implementation embedded in an existing ES implementation, in order to make the results as stable as possible, to avoid biasing the results to a particular ES implementation, to encourage contributors, and to focus on the performance differences in the hash table implementations by eliminating all other performance effects as much as possible.
- The program runs each benchmark many different times in order to produce enough numbers that noise is visually obvious in the resulting graph. (Most of the speed graphs are nice and smooth.)
Results
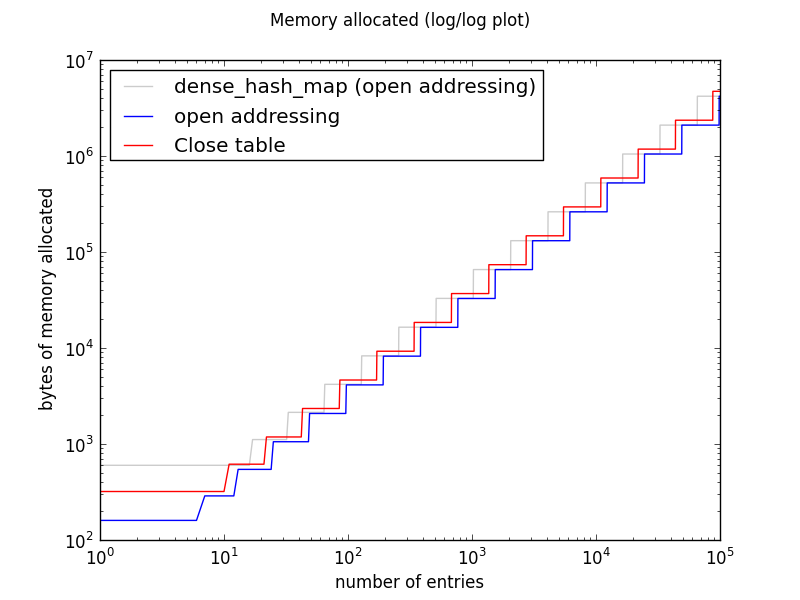
Memory usage
All three implementations double the size of the table whenever it gets too full. On a log-log plot, this shows as stair-steps of a constant height. The slope of each staircase is 1, indicating linear growth.
Both OpenTable and CloseTable are much more memory-efficient than DenseTable, because dense_hash_map is tuned for fast lookups at all costs.
For any N > 5, a CloseTable with N entries allocates either 1.0625x or 2.125x as much memory as an OpenTable with N entries (1.125x or 2.25x as much memory on 64-bit systems). Both tables double in size at certain thresholds, and the thresholds for CloseTable are lower than those for OpenTable. That is, as a CloseTable is populated, it doubles in size sooner than the corresponding OpenTable. The factors determining this behavior are (1) the fact that CloseTable entries are 50% larger, and it therefore takes fewer of them to fill up a power-of-two-sized allocation; and (2) the value of OpenTable::max_fill_factor().
It is tempting to reduce this complicated picture to a single number, and write that CloseTables are, for example, 20% larger. Or 30%. But such a number would not be easily justified mathematically: the ratio does not converge as the number of entries increases.
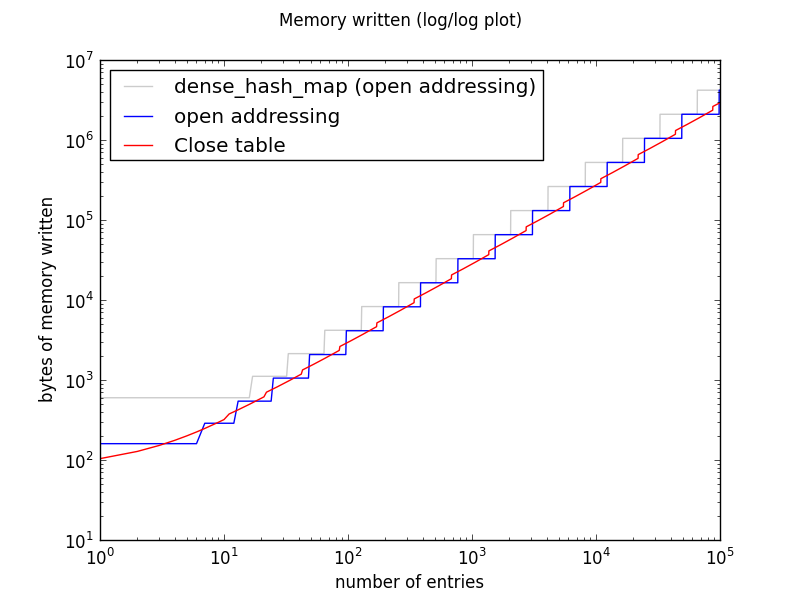
DenseTable and OpenTable must initialize the entire table each time they resize. CloseTable also allocates large chunks of memory, but like a vector, it does not need to write to that memory until there is data that needs to be stored there.
This means that for a huge Map with no delete operations, a Close table could use more virtual memory but less physical memory than its open addressing counterparts. This will not be the only use case that stresses memory usage, though. Applications may also create many small tables and may delete entries from large tables.
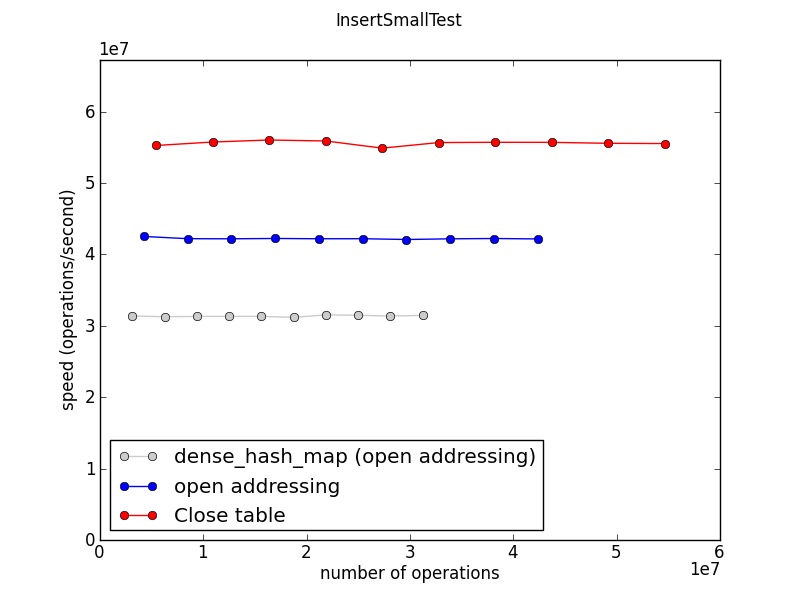
Insertion speed
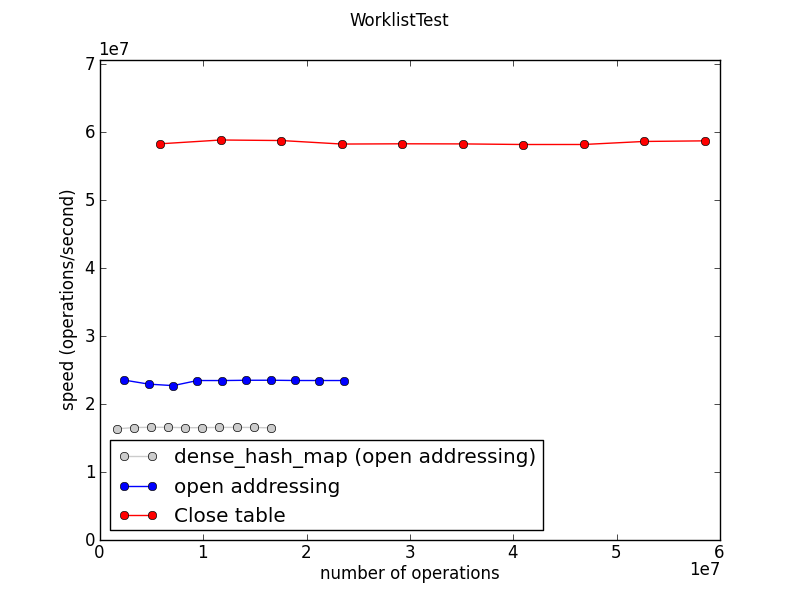
This measures the time required to fill a table to about 100 entries, repeatedly. (The “1e7” on the axes indicates that the numbers are in tens of millions: the Close table is doing about 60 million inserts per second on this machine.)
This graph and the following ones show speed, so higher is better.
Ideally all these graphs would show three straight horizontal lines, indicating that all three implementations scale beautifully to large work loads. And indeed this seems to be the case, mostly.
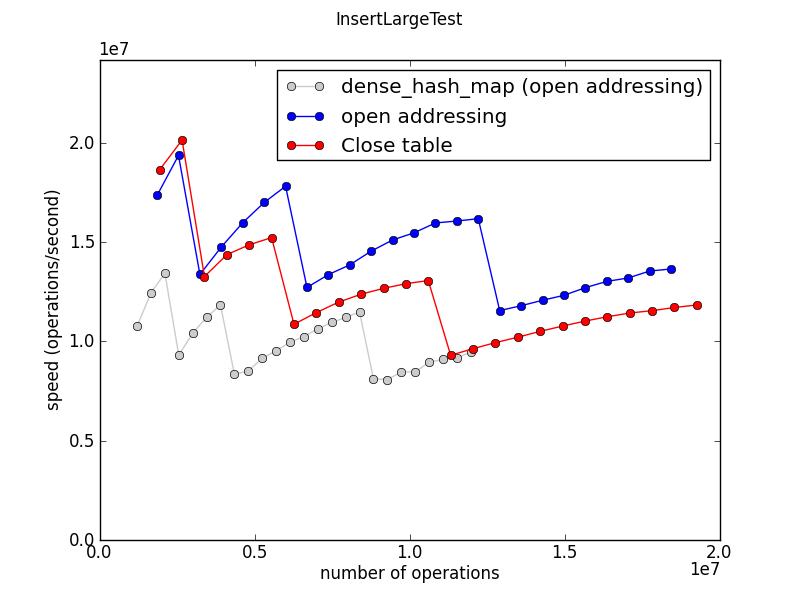
This test measures the time required to fill a single gigantic table.
The jagged shape of this graph is robust. It reflects the fact that the table doubles in size as it grows, and rehashing is a significant part of the expense of populating a huge table.
Lookup speed
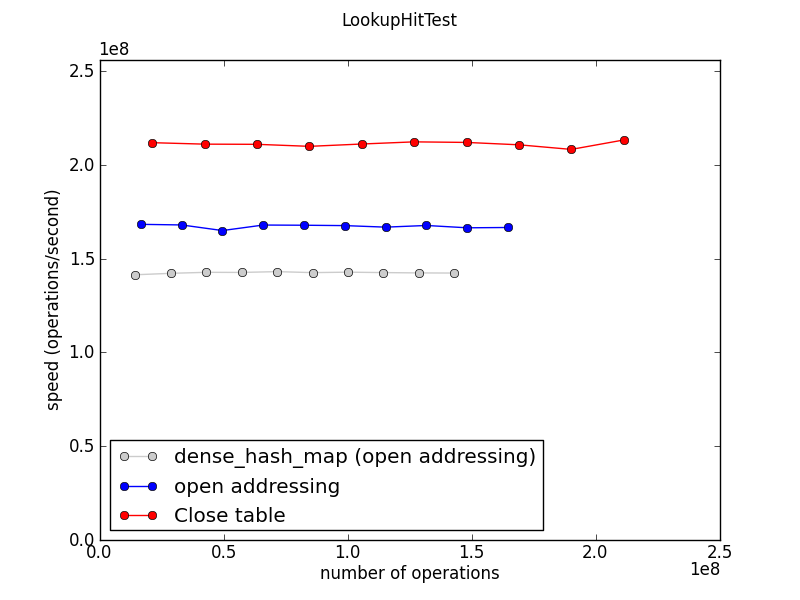
This test measures the speed of table.get(k) operations, where k is the key of an existing entry in the table.
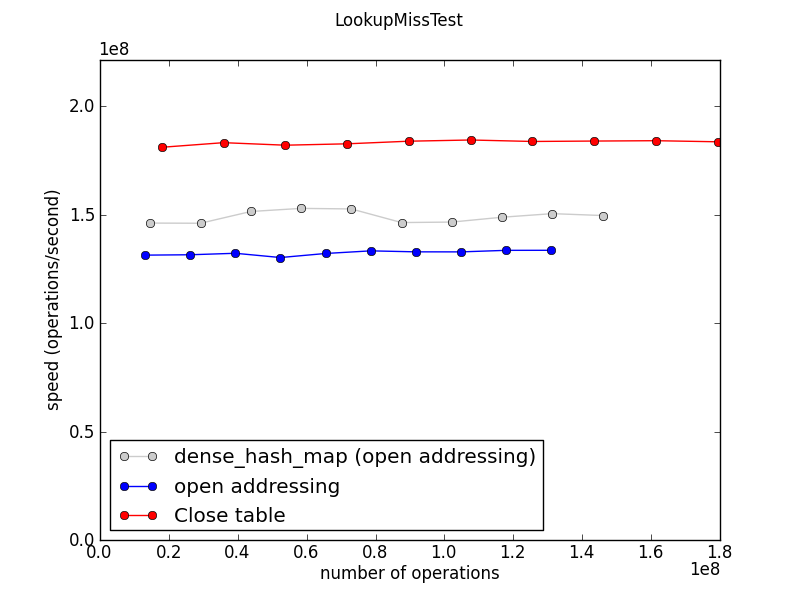
This test measures the speed of table.get(k) operations, where the key k is not found in the table.
In an OpenTable, lookups that miss are slower than lookups that hit when there is at least one collision. This is because we keep probing the hash table until we find an empty entry.
DenseTable is only slightly slower for misses, perhaps because more lookups have zero collisions. (?)
Deletion speed
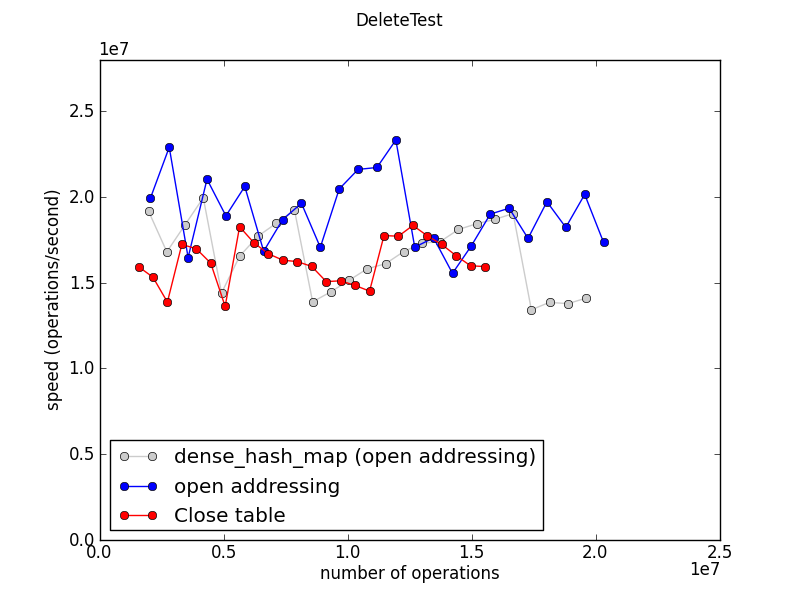
This test creates a table with 700 entries, then measures the speed of alternately adding an entry and deleting the oldest remaining entry from the table. Entries are therefore removed in FIFO order. Each “operation” here includes both an insert and a delete.
The CloseTable stores the entries in insertion order, so this test gets extremely good memory locality. The effect is even more pronounced in a 32-bit build.
This test measures the speed of deleting all entries from a very large table.
The numbers for dense_hash_map are jagged because DenseMap shrinks the table at certain threshold sizes as entries are deleted, and shrinking the table is expensive.
The apparent randomness of the OpenTable and CloseTable numbers is reproducible and unexplained.
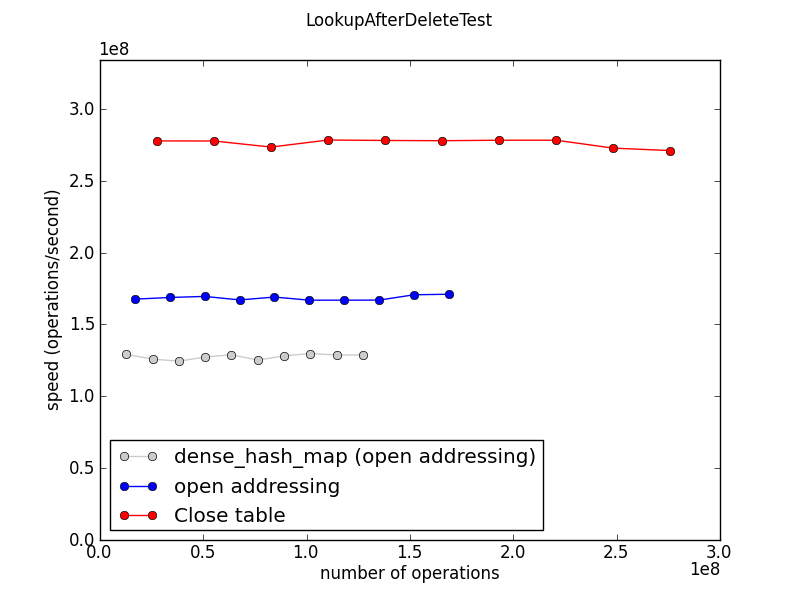
This test measures the performance of lookups, mostly misses, in a table that was filled to size 50000, then reduced to size 195 by deleting most of the entries.
The results here are sensitive to the two sizes, which are totally arbitrary choices. A less arbitrary replacement for this test would be welcome.